Tracking The Sun for More Energy
Prof. M. A. L. A. Haleem & Group

INTRODUCTON
The sun has been a major source of energy for ages. However, the solar energy is still a small fraction of our total energy consumption due to inadequate advances in low cost, highly efficient solar energy harvesting systems. To harvest maximum energy, the collecting devices should be directly pointed to the sun throughout the day i.e., the sun should be tracked (Nsengiyumva 2018).
There are two types of solar trackers according to their degrees of freedom, namely single axis and dual axis trackers. While dual axis solar trackers produce the best results (Khalifa 1998), single axis trackers may collect most of the energy that can be harvested and is a cost-effective solution in some cases. Trackers are used in devices which may convert solar energy either into electrical energy (Senpinar 2012) or thermal energy (Elashmawy 2020). Figure 1 illustrates the use of single axis and dual axis trackers in solar energy harvesting systems. Sun path computation algorithm is an essential component in the design and construction of solar trackers. Formulation and implementation of sun path algorithm have to be carried out considering limited processing power, memory, and latencies of the microcontrollers in the embedded systems. (Er 2018).


(a) (b)

(c)
Figure 1. Solar trackers (a) single axis trackers used in PV systems (b) dual axis trackers used in PV systems (c) reflective parabolic concentrator with tracking for solar-thermal energy harvesting.
SUN’S PATH IN THE SKY
The apparent position of the sun in the sky at any time and day is expressed by a pair of coordinates. As illustrated in Figure 2, the altitude angle (ALT) is measured from the horizon upward and the azimuth angle (AZ) with respect to north (N) towards east. The direction of the sun with respect to zenith, the point in the sky right above is the zenith angle (φ) and this angle is complementary to the azimuth angle. The sun path is the variation of position in the sky as time passes during the day.

Figure 2. Position of the sun in the sky as seen by an observer on earth. Zenith is the point directly above the observer. Altitude angle with respect to the horizon and the azimuth angle from the describes the position of sun (N).
A. Primers of sun path
In the study of sun path algorithms, we come across a number of terminologies related to astronomy and geography. Review of the preliminaries of earth’s orbit facilitates the comprehension of these terminologies. Subsequently, one can grasp the frames of references and coordinate systems of solar geometry involved in the computation of sun path.
The earth orbits the sun in an elliptical path, completing a cycle in a year as shown in Figure 3. The plane of orbit is known as ecliptic. The rotational axis of earth is tilted by approximately 23.5o towards the ecliptic. For an observer on earth, the sun moves from east to west in the sky daily (diurnal motion) as shown in Figure 4 due to earth’s rotation around its axis. The sun path is vertical to the horizon at earth’s equator (0o latitude) but tilted at other places by the latitude angle of the location. The sun path shifts daily in the north-south direction. Around March 21st and September 23rd, the sun rises directly from east and sets directly in the west. The path has the maximum shift to the north on June 21st and the maximum shift to the south on December 22nd.
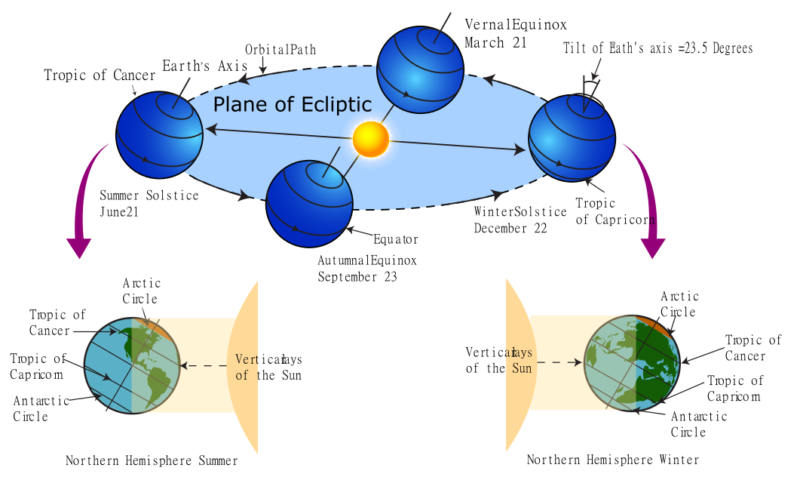
Figure 3. Earth’s orbit around the sun.



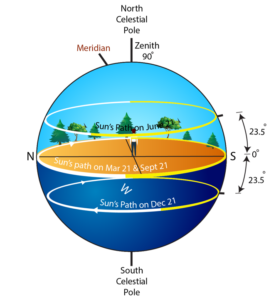
Figure 4. Sun paths on the days of different seasons at different geographical locations. Three paths shown in each figure are at summer solstice, equinoxes and winter solstice. The angle of sun path with the horizon is complementary to the local latitude. Shown from left to right and top to bottom are sun paths for locations;(a) at the equator (0olatitude), (b) at 7o N as in Sri Lanka, (c) 40o N, and (d) at the north pole (90o N).
B. Celestial Globe and Frames of references
Celestial globe is the globe of sky we perceive when observed from the earth. The objects in the sky including the sun moves on the celestial globe. As shown in Figure 5, the north celestial pole is directly above earth’s north pole. Likewise, south celestial pole is directly above the south pole of the earth. Therefore, the celestial objects at the celestial poles are fixed with respect to an observer on earth. Celestial globe can be marked with declination and right ascension, which are the outward projections of latitudes and longitudes of the terrestrial globe on to the celestial globe. The terrestrial equator (latitude 0o) and the celestial equator are in the same plane. The sun shifts among stars with a yearly cycle on the celestial globe on a path known called ecliptic at a tilt of 23.5o with celestial equator.

Figure 5. Celestial globe and the sun’s path known as ecliptic.
There are three frames of reference and hence coordinate systems involved in the process of calculating sun path namely celestial (equatorial), ecliptic, and horizon frames of reference. The celestial and ecliptic frames of reference are earth centric and the origin is at the center of earth. The ecliptic frame of reference is at an angle of 23.5o with the equatorial frame of reference. The horizon frame of reference (an observer’s frame of reference) depends on the latitude of the observer on the earth. As illustrated in Figure 6, for the observer on earth, the celestial north is oriented at an angle equal to the latitude angle of his/her location with respect to the horizon. Zenith is the point on the celestial globe directly above the observer.
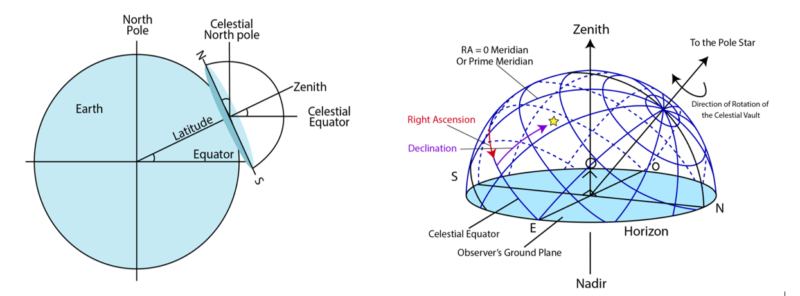
Figure 6. Horizon frame of reference. (a) zenith of an observer makes an angle equal to the latitude of the observer with the equator. The celestial north pole is observed at an angle equal to the latitude from the northern horizon. (b) celestial globe and horizon as seen by the observer on the earth.
Sun path computation algorithms are realized by considering transformation of coordinates from one frame of reference to another (Szokolay 2007). The starting point is the ecliptic frame of reference. The sun’s position on the ecliptic on a given day is found by considering the day of the solar year starting with the vernal equinox, which is the day on which the ecliptic crosses the celestial equator. Then the ecliptic coordinates are transformed to celestial coordinates in terms of right ascension, a and declination, d. Eventually a transformation takes place to horizon coordinates in terms of altitude and azimuth. Figure 7 illustrates the coordinate transformation from celestial (equatorial) frame of reference to horizon frame of reference. S indicates the direction of sun and P indicates the location of observer on earth. The equatorial coordinates are (x, y, z). The horizon frame of reference (E, N, Z) has been translated (shifted) to (E’, N’, Z’) to facilitate the coordinate transformation. A hemisphere of radius r is assumed in the analysis. The angle ω made by the sun in the azimuth with the direction of solar noon, is the hour angle.

Figure 7. The rotated equatorial and ALT-AZ frames of references. Spherical and cartesian coordinates of the sun are indicated.
C. Real time to solar time
The time we read on our real time clock (RTC) is different from the solar time relevant to the calculation of sun position. For example, solar noon implies the time at which sun is on the local meridian, an imaginary circle passing through the north point on the horizon, through the celestial pole, up to the zenith, and through the south point on the horizon. Local meridian is perpendicular to the local horizon. The real time at solar noon may not be 12:00 PM. Solar time varies continuously with the location at a given moment of time whereas the real time is same anywhere in the time zone of your location. To calculate sun position, real time is converted to solar time by taking into account the difference between average local meridian and the actual local meridian. The formulations also compensate for yearly shift of vernal equinox.
FORMULATIONS FOR SUN’ POSITION CALCULATION
The solar path calculation proceeds as follows.
- Compute right ascension (RA) α:
(1)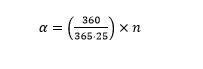
where n is the number of days since last vernal equinox. [This is an approximation to the actual value. The fact that the sun is moving on the ecliptic rather than the celestial equator, makes the exact variation of RA non-uniform. The eccentricity of the elliptical orbit of earth around the sun causes non-uniform motion on the ecliptic as well. A more precise approach includes equation of time, a compensation factor].
- Compute the local solar time ts in hours at local longitude using a real time clock reading tr. The real time tr is synchronized to the Coordinated Universal Time (UTC).
(2)![]()
where Z is the time offset for the local time zone and DS = 1h if day light saving is in effect and DS = 0 otherwise.
(3)
where Lst is the standard longitude of the time zone and Lloc is the local longitude. Longitudes are positive eastward from prime meridian where prime meridian is the longitude passing through Greenwich. The time zone is in hours from UTC (Sri Lankan Time = UTC + 5.5 hours).
- Find the hour angle ω using (4)

- Compute declination δ using (5)

where o is the angle of ecliptic with respect to the celestial equator.
- Compute ALT and AZ of the sun using δ, ω, and φ using
(6) ![]()
(7) ![]()
correct quadrant for AZ should be identified considering the signs of
(8) ![]()
(9) ![]()
Although the above algorithm is simple to implement except for the trigonometric functions involved, the day of vernal equinox should be an input to the algorithm. For the six years starting with year 2020, the vernal equinox occurs on March 20th. The time of the events in UT time are given in TABLE 1.
TABLE 1. UTC time of vernal equinoxes on Earth for the years 2020-2025. The day of event is March 20th for all six years.
| Year | Time (24 h) |
| 2020 | 03:50 |
| 2021 | 09:37 |
| 2022 | 15:33 |
| 2023 | 21:24 |
| 2024 | 03:07 |
| 2025 | 09:02 |
Computation of event times in this table is based on the algorithms from (Meeus 1998) . Extensive table of calculated times for equinoxes and solstices are available online (Espenak 2018).
CONCLUSION
Sun path calculation is an essential component in solar tracking systems. A solar tracking system computes the direction of the sun at a given time of the day and rotates the altitude and azimuth motors to directly face the sun. This process maximizes the amount of solar energy harvested on a day. Knowledge of celestial mechanics of earth’s rotation and the orbit around the sun, frames of reference in astronomy, concepts of time measures are used in formulating a sun path algorithm. This article introduced the primers of celestial motion, the geometry, and the frames of references involved in the computation of sun path. Hence, we discussed a step-by-step process of calculating the position of the sun. This work has been a part of solar tracking algorithm development and implementation as a program in a microcontroller embedded in the solar tracker prototyped at South Eastern University of Sri Lanka.
REFERENCES
Elashmawy, M. 2020. “Improving the performance of a parabolic concentrator solar tracking tubular solar still (PCST-TSS) using gravel as a sensible heat storage material.” The Int. J. Sci. and Tech. of Desalting and Water Purification, Elsevier, Vol. 1.
Er, Z. and Marangozoglu, S. 2018. “New Design for Solar Panel Tracking System Based on Solar Calculations.” IEEE 61st International Midwest Symposium on Circuits and Systems (MWSCAS).
Espenak, Fred. 2018. www.astropixels.com/ephemeris/ soleq2001.html.
Khalifa, A. J. N. and Al-Mutawalli, S. S. 1998. “Effect of Two-Axis Sun Tracking on the Performance of Compound Parabolic Concentrators.” Energy Conversion and Management, Vol. 39, No. 10 1073–1079.
Meeus, J. 1998. Astronomical Algorithms, Second edition . Richmond, Virginia, USA: Willmann-Bell, Inc.
Nsengiyumva, W. et. al. 2018. “Recent Advancements and Challenges in Solar Tracking Systems (STS): A Review.” Renewable and Sustainable Energy Reviews, vol. 81 250–279.
Senpinar, M. Cebaci, A. 2012. “Evaluation of Power Output for Fixed and Two-Axis Tracking PV arrays.” Applied Energy 92: 677–685.
Szokolay, S. V. 2007. Solar geometry, PLEA NOTES-1, 2nd ed. The University of Queensland, Brisbane.









